Optimal Threshold vs. Upsampling

Dealing with Unbalanced Data

Machine Learning
Classification
Author

Arcenis Rojas

Published

February 15, 2023

Introduction

In any binary classification analysis it is common to have to deal with heavily unbalanced data, i.e., the frequency of the majority class in the dependent variable is overwhelmingly greater than that of the minority class. One of the main reasons this can be problematic is that many classification algorithms are biased toward the majority class. If 95% of the observations belong to the majority class in the training data and the algorithm always predicts the majority class, then it will have achieved 95% accuracy.

There are many ways of dealing with unbalanced data including changing from a classification algorithm to an anomaly detection algorithm like an isoforest or a one-class SVM, using SMOTE to re-balance the data sets in pre-processing, up- or down-sampling, and changing the classification threshold. Here I will only deal with up-sampling and changing the classification threshold to see how it affects classification metrics by way of going through an exercise. I’ll first create and tune a base model then do the same for an up-sampled model using Tidymodels (Kuhn and Wickham 2020). Hyperparameter tuning will be done with the finetune package (Kuhn 2023a). I’ll then find the optimal threshold for each using the probably package (Kuhn, Vaughan, and Ruiz 2023). Finally I’ll show a comparison of their respective classification metrics.

Code 
library(tidyverse)
library(tidymodels)
library(colino)
library(themis)
library(finetune)
library(probably)
library(skimr)
library(knitr)
library(kableExtra)

conflicted::conflict_prefer("filter", "dplyr")
conflicted::conflict_prefer("select", "dplyr")
tidymodels_prefer()

Lending Club Data

For this project I’ll be using the lending_club data set from the modeldata (Kuhn 2023b) package. The data contain the Class variable which indicates whether a loan was “good” or bad”. For the purposes of this analysis I also will consider the “bad” outcome as the event to predict.

Data Exploration

The first step is to load the data using the readr package from the Tidyverse (Wickham et al. 2019) and summarize it using the skimr package (Waring et al. 2022).

Code 
data("lending_club", package = "modeldata")

skim(lending_club) |> select(-complete_rate)
Data summary
Name lending_club
Number of rows 9857
Number of columns 23
_______________________
Column type frequency:
factor 6
numeric 17
________________________
Group variables None

Variable type: factor

skim_variable n_missing ordered n_unique top_counts
term 0 FALSE 2 ter: 7047, ter: 2810
sub_grade 0 FALSE 35 C1: 672, B5: 624, A1: 612, B3: 607
addr_state 0 FALSE 50 CA: 1324, TX: 900, NY: 767, FL: 731
verification_status 0 FALSE 3 Sou: 3742, Not: 3434, Ver: 2681
emp_length 0 FALSE 12 emp: 3452, emp: 893, emp: 769, emp: 733
Class 0 FALSE 2 goo: 9340, bad: 517

Variable type: numeric

skim_variable n_missing mean sd p0 p25 p50 p75 p100 hist
funded_amnt 0 15683.56 8879.11 1000.00 8500.00 15000.00 21000.00 40000.00 ▆▇▅▃▂
int_rate 0 12.53 4.89 5.32 8.49 11.99 15.31 28.99 ▇▇▃▂▁
annual_inc 0 80320.36 53450.17 0.00 50000.00 68900.00 96000.00 960000.00 ▇▁▁▁▁
delinq_2yrs 0 0.33 0.89 0.00 0.00 0.00 0.00 22.00 ▇▁▁▁▁
inq_last_6mths 0 0.58 0.88 0.00 0.00 0.00 1.00 5.00 ▇▁▁▁▁
revol_util 0 51.73 24.38 0.00 33.20 51.80 70.40 144.30 ▅▇▇▂▁
acc_now_delinq 0 0.01 0.08 0.00 0.00 0.00 0.00 2.00 ▇▁▁▁▁
open_il_6m 0 2.75 2.93 0.00 1.00 2.00 3.00 32.00 ▇▁▁▁▁
open_il_12m 0 0.74 1.01 0.00 0.00 0.00 1.00 20.00 ▇▁▁▁▁
open_il_24m 0 1.62 1.70 0.00 0.00 1.00 2.00 30.00 ▇▁▁▁▁
total_bal_il 0 35286.92 41923.62 0.00 9450.00 23650.00 46297.00 585583.00 ▇▁▁▁▁
all_util 0 60.31 20.28 0.00 47.00 62.00 75.00 198.00 ▂▇▂▁▁
inq_fi 0 0.93 1.47 0.00 0.00 0.00 1.00 15.00 ▇▁▁▁▁
inq_last_12m 0 2.19 2.44 0.00 0.00 2.00 3.00 32.00 ▇▁▁▁▁
delinq_amnt 0 12.17 565.47 0.00 0.00 0.00 0.00 42428.00 ▇▁▁▁▁
num_il_tl 0 8.64 7.52 0.00 4.00 7.00 11.00 82.00 ▇▁▁▁▁
total_il_high_credit_limit 0 45400.75 45103.21 0.00 16300.00 34375.00 60786.00 554119.00 ▇▁▁▁▁

The above data summary shows some important things. First, there are 9,857 observations and 23 variables with no missing values. Also, the data has 6 factor variables and 17 numeric variables. It shows that most of the numeric variables are left skewed. The “sub_grade” and “addr_state” factor variables have 35 and 50 levels respectively. With so many unique values it’s very likely that some of the classes in each of those variables become overwhelmed by majority classes. While there are feature engineering steps that I can take such as consolidating infrequent classes or splitting up sub_grade into constituent parts, I’ll just allow the feature selection step to handle it. Finally, the “Class” factor variable (dependent variable) has two levels with the majority class – “good” – having 9,340 observations and the minority class – “bad” – having 517 observations.

Here I’ll just look at the proportions of the Class variable.

Code 
lending_club |>
  ggplot(aes(y = Class)) +
  geom_bar(aes(x = (..count..) / sum(..count..))) +
  scale_x_continuous(labels = scales::percent) +
  labs(
    x = "Proportion",
    y = NULL,
    title = "Frequency of loan outcome categories (Class)"
  ) +
  theme_bw() +
  theme(plot.title = element_text(hjust = 0.5))

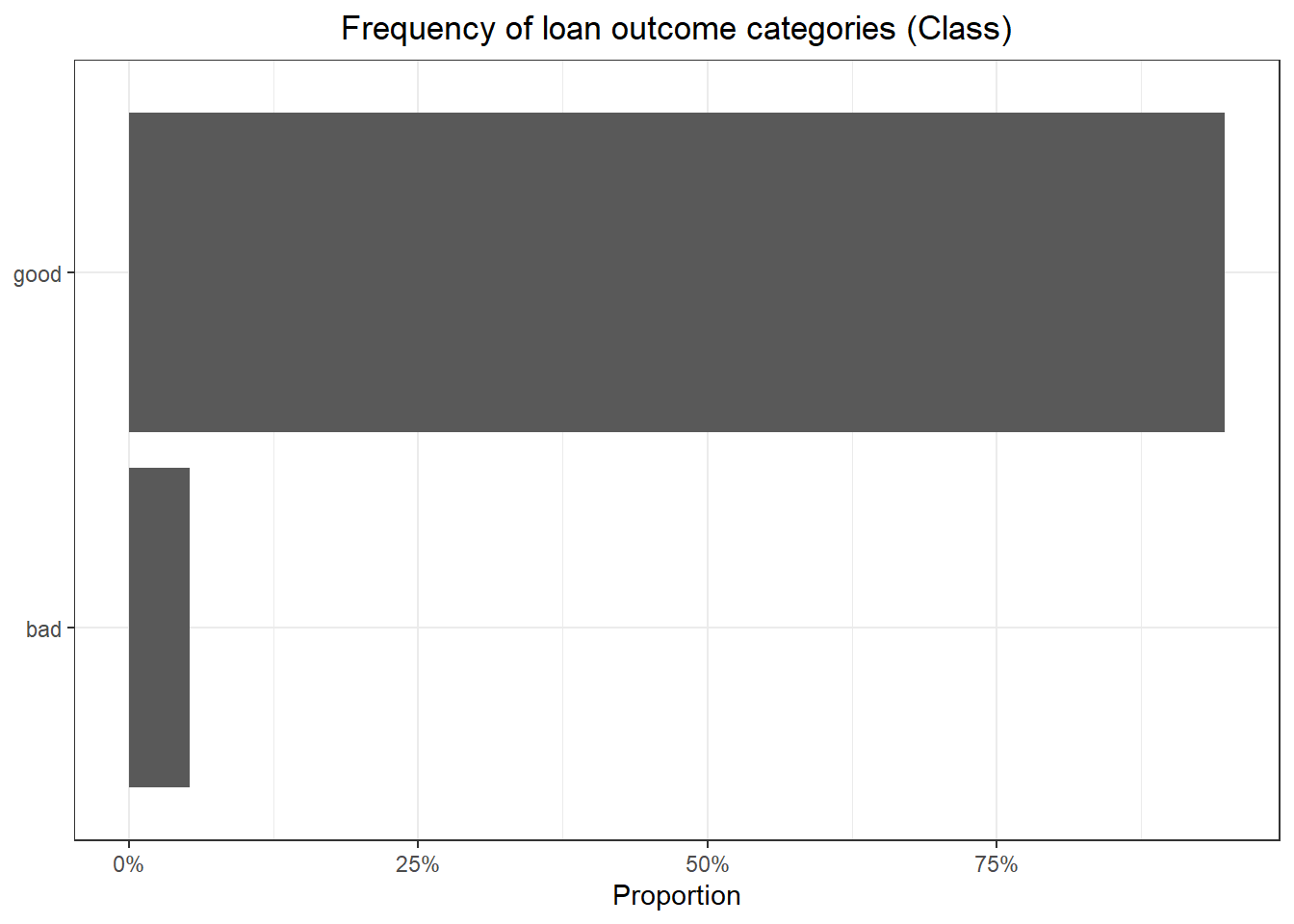
Here we see a sever class unbalance with only about 5% of loans having a “bad” outcome.

Create Data Splits and Other Common Elements

For the analysis I’ll split the data into training (75%) and test (25%) sets stratified by the Class variable. I’ll then create 100 bootstraps of the training data for model tuning, also stratified by the Class variable. Stratification will ensure that both cuts of the data and the bootstraps retain the class unbalance as close to the proportions of the original data.

Here I also create a list of features to control the model tuning process.

Code 
# Create training/test split
set.seed(95)
tt_split <- initial_split(lending_club, prop = 0.75, strata = Class)

# Create the bootstrap object
set.seed(386)
bstraps <- bootstraps(training(tt_split), times = 100, strata = Class)

# Create the model object for the workflows
lr_mod <- logistic_reg(mode = "classification", engine = "glm")

# Create a list of control options
race_control <- control_race(
  verbose = FALSE,
  allow_par = FALSE,
  burn_in = 3,
  save_workflow = TRUE,
  save_pred = TRUE
)

Train Base Model

The base recipe will perform the following steps:

  1. Remove variables with near-zero variance

  2. Scale and center all numeric variables

  3. Convert categorical variables to dummy variables

  4. Select variables based on mRMR using the colino package (Pawley, Kuhn, and Jacques-Hamilton 2023); the percentile threshold used to decide which variables to keep will be chosen through model tuning

The base recipe will be combined with a logistic regression model specification to put into a workflow. This workflow then goes through a Bayesian hyperparameter tuning process to find the best mRMR threshold as mentioned above. “Best” is defined as the full model specification that yields the highest area under the receiver operator curve (ROC-AUC) because I’ll be choosing the optimal probability threshold on the basis of this curve, even though it would be preferable to choose on the basis of the area under the precision-recall curve (PR-AUC) with unbalanced data. (Rosenberg 2022)

Code 
# Create a base recipe
base_rec <- recipe(Class ~ ., data = training(tt_split)) |>
  step_nzv(all_predictors()) |>
  step_normalize(all_numeric_predictors()) |>
  step_dummy(all_nominal_predictors(), one_hot = FALSE) |>
  step_select_mrmr(
    all_predictors(),
    threshold = tune(),
    outcome = "Class"
  )

# First tune the base model to get the best set of variables with MRMR
base_wflow <- workflow() |> add_recipe(base_rec) |> add_model(lr_mod)

set.seed(40)
base_tuned <- tune_race_win_loss(
  base_wflow,
  resamples = bstraps,
  control = race_control,
  grid = 10,
  metrics = metric_set(pr_auc, roc_auc, accuracy)
)

# Get the workflow with the best MRMR threshold
best_base <- select_best(base_tuned, "roc_auc")

# Get the MRMR threshold from the best base model
mrmr_threshold <- best_base |> pull(threshold)

The mRMR threshold associated with the best model is 0.9478018 .

Train Upsampled Model

The upsampled model will only add the pre-processing step of upsampling the minority class to the same proportion as the majority class (or close to it) by resampling observations with a Class value from the minority class using the themis package (Hvitfeldt 2023). To ensure that this is the only difference, I’ll take the mRMR threshold that was tuned for the base model directly from the best base model and specify it as the threshold for the upsampling model.

Code 
# Build a recipe for upsampling by first updating the MRMR step from the base recipe with the threshold from the tuning process then adding upsampling
upsample_rec <- base_rec
select_mrmr_step <- tidy(upsample_rec) |>
  filter(type %in% "select_mrmr") |>
  pull(number)

upsample_rec$steps[[select_mrmr_step]] <- update(
  upsample_rec$steps[[select_mrmr_step]],
  threshold = mrmr_threshold
)

upsample_rec <- upsample_rec |>
  step_upsample(Class, over_ratio = tune())

# Create the upsample workflow object
upsample_wflow <- workflow() |> add_recipe(upsample_rec) |> add_model(lr_mod)

# Tune the workflow containing the upsample recipe
set.seed(40)
upsample_tuned <- tune_race_win_loss(
  upsample_wflow,
  resamples = bstraps,
  control = race_control,
  grid = 10,
  metrics = metric_set(pr_auc, roc_auc, accuracy)
)

# Get the workflow with the best MRMR threshold
best_upsample <- select_best(upsample_tuned, "roc_auc")

The best over-sampling ratio is 1.1065577 .

Compare Model Classification Metrics

Now that I’ve run both models and gotten the best hyperparameters for each, I’ll finalize both models and ensure that I have the same sets of variables in the models.

Code 
# Get evaluation datasets for both workflows
set.seed(75)
eval_base <- base_wflow |>
  finalize_workflow(best_base) |>
  last_fit(tt_split)

# Build the evaluation tibble for the upsample case
set.seed(212)
eval_upsample <- upsample_wflow |>
  finalize_workflow(select_best(upsample_tuned, "roc_auc")) |>
  last_fit(tt_split)

eval_base |>
  extract_fit_engine() |>
  tidy() |>
  select(base = term) |>
  bind_cols(
    eval_upsample |>
      extract_fit_engine() |>
      tidy() |>
      select(upsample = term)
  ) |>
  kable(booktabs = TRUE) |> 
  kable_styling("striped")
base upsample
(Intercept) (Intercept)
int_rate int_rate
inq_last_6mths inq_last_6mths
open_il_12m open_il_12m
sub_grade_G4 sub_grade_G4
addr_state_SD addr_state_SD
verification_status_Verified verification_status_Verified

The above table shows that both models ended up with the same sets of variables. Next we’ll find the optimal threshold cut-offs for each set of predictions on the test data using Youden’s J-Index.

Code 
base_preds <- tibble(
  truth = collect_predictions(eval_base) |> pull(Class),
  estimate = collect_predictions(eval_base) |> pull(.pred_bad),
  pred_class = collect_predictions(eval_base) |> pull(.pred_class)
)

# Find the optimal classification threshold for the base model
opt_thresh_base <- base_preds |>
  threshold_perf(truth, estimate, seq(0, 1, length.out = 1000)) |>
  filter(.metric %in% "j_index") |>
  slice_max(.estimate, with_ties = FALSE) |>
  pull(.threshold)

upsample_preds <- tibble(
  truth = collect_predictions(eval_upsample) |> pull(Class),
  estimate = collect_predictions(eval_upsample) |> pull(.pred_bad),
  pred_class = collect_predictions(eval_upsample) |> pull(.pred_class)
)

# Find the optimal classification threshold for the upsample model
opt_thresh_upsample <- upsample_preds |>
  threshold_perf(truth, estimate, seq(0, 1, length.out = 1000))|>
  filter(.metric %in% "j_index") |>
  slice_max(.estimate, with_ties = FALSE) |>
  pull(.threshold)

The optimal probability threshold for classifying a loan as bad with the base model is 0.0550551 and that for the upsampling model is 0.5525526

Each table of predictions currently has 3 columns showing the actual class for a given observation (truth), the prediction probability associated with that observation being a bad loan (estimate), and a predicted class based on a probability threshold of 0.5 (pred_class). The table below shows the first few predictions from the base model.

Code 
base_preds |>
  slice_head(n = 10) |>
  kable(booktabs = TRUE) |>
  kable_styling("striped")
truth estimate pred_class
good 0.0350714 good
good 0.0107027 good
good 0.0297951 good
good 0.0432709 good
good 0.0335889 good
good 0.0310299 good
good 0.0452632 good
good 0.0226798 good
good 0.0170578 good
good 0.0286983 good

Now I’d like to add to each of these tables another column containing the predicted class based on the optimal probability threshold for each respective table. The below table shows a few cases for which the predicted class using a 0.5 probability threshold does not match the predicted class using the optimal probability threshold of 0.5525526 .

Code 
base_preds <- base_preds |>
  mutate(
    opt_pred_class = if_else(estimate >= opt_thresh_base, "bad", "good") |>
      factor(levels = c("bad", "good"))
  )

upsample_preds <- upsample_preds |>
  mutate(
    opt_pred_class = if_else(
      estimate >= opt_thresh_upsample,
      "bad",
      "good"
    ) |>
      factor(levels = c("bad", "good"))
  )

upsample_preds |> 
  filter(opt_pred_class != pred_class) |>
  slice_head(n = 10) |>
  kable(booktabs = TRUE) |>
  kable_styling("striped")
truth estimate pred_class opt_pred_class
good 0.5030688 bad good
bad 0.5284232 bad good
good 0.5373165 bad good
good 0.5007787 bad good
good 0.5173375 bad good
good 0.5463947 bad good
bad 0.5297278 bad good
good 0.5227147 bad good
good 0.5284232 bad good
good 0.5284232 bad good

Next I’ll plot confusion matrices for each set of predictions.

Code 
conf_mats <- list(base = base_preds, upsample = upsample_preds) |>
  map(
    \(x) list(
      conf_mat(x, truth = truth, estimate = pred_class),
      conf_mat(x, truth = truth, estimate = opt_pred_class)
    ) |>
      set_names("standard", "optimal")
  ) |>
  list_flatten()

conf_mat_plots <- conf_mats |>
  imap(
    \(x, y) {
      plot_title <- str_replace(y, "_", " ") |>
        str_to_title()
      
      autoplot(x, type = "heatmap") +
        ggtitle(plot_title) +
        theme(plot.title = element_text(hjust = 0.5))
    }
  )

cowplot::plot_grid(plotlist = conf_mat_plots)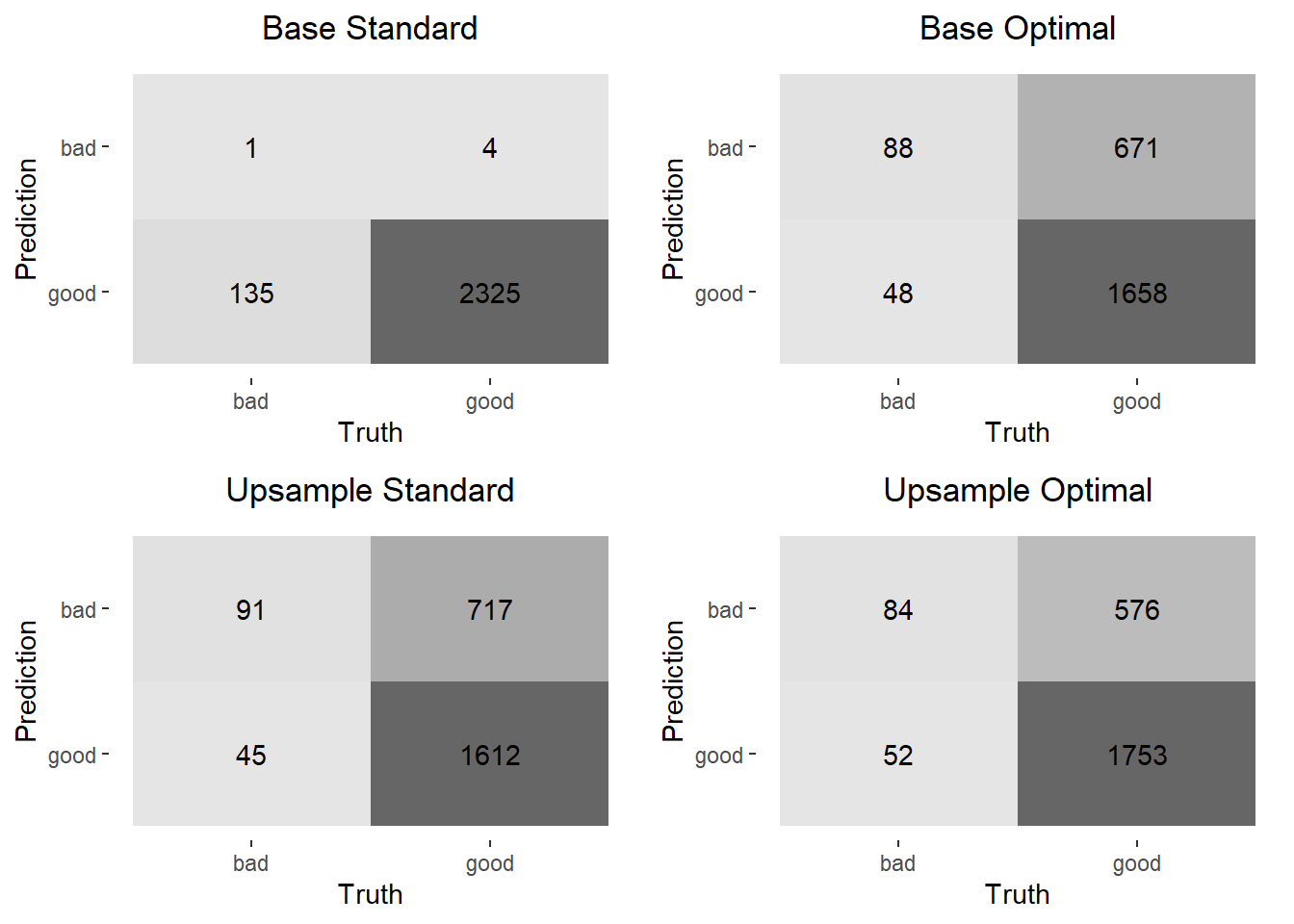

The above confusion matrices show that both changing the probability threshold for classification as a bad loan and upsampling have a significant impact on the number of positive predictions (“bad” loan), even though most of those are predicted incorrectly with this model. It’s also interesting to note that doing both – changing the probability threshold and upsampling – shows very little improvement over doing just one or the other. Below are some classification metrics for each model specification.

Code 
conf_mats |>
  imap(
    \(x, y) summary(x) |>
      select(-.estimator) |>
      set_names("metric", str_replace(y, "_", " ") |> str_to_title())
  ) |>
  reduce(left_join, by = "metric") |>
  kable(booktabs = TRUE) |>
  kable_styling("striped")
metric Base Standard Base Optimal Upsample Standard Upsample Optimal
accuracy 0.9436105 0.7083164 0.6908722 0.7452333
kap 0.0103118 0.1137115 0.1086066 0.1316040
sens 0.0073529 0.6470588 0.6691176 0.6176471
spec 0.9982825 0.7118935 0.6921426 0.7526836
ppv 0.2000000 0.1159420 0.1126238 0.1272727
npv 0.9451220 0.9718640 0.9728425 0.9711911
mcc 0.0285977 0.1775336 0.1757144 0.1909560
j_index 0.0056355 0.3589523 0.3612602 0.3703306
bal_accuracy 0.5028177 0.6794762 0.6806301 0.6851653
detection_prevalence 0.0020284 0.3079108 0.3277890 0.2677485
precision 0.2000000 0.1159420 0.1126238 0.1272727
recall 0.0073529 0.6470588 0.6691176 0.6176471
f_meas 0.0141844 0.1966480 0.1927966 0.2110553

The first thing that one might notices from the above is how high the accuracy is for the base model. It’s important to remember, though, that when a data set is so unbalanced all a model has to do is predict the majority class all the time and it will have high accuracy. That model, though, has a very low sensitivity and high specificity. The high specificity, again, is due to the fact that the actual data has an overwhelming proportion of the majority class. Looking across at the metrics for the other models one sees drops in both accuracy and specificity, but much more significant increases in sensitivity from the base model. It’s also useful to note that other metrics like balanced accuracy, kappa, mcc, and f_measure also improve. This is further evidence of the effect that the imbalance in classes has on the base model.

References

Hvitfeldt, Emil. 2023. “Themis: Extra Recipes Steps for Dealing with Unbalanced Data.” https://CRAN.R-project.org/package=themis.
Kuhn, Max. 2023a. “Finetune: Additional Functions for Model Tuning.” https://CRAN.R-project.org/package=finetune.
———. 2023b. “Modeldata: Data Sets Useful for Modeling Examples.” https://CRAN.R-project.org/package=modeldata.
Kuhn, Max, Davis Vaughan, and Edgar Ruiz. 2023. “Probably: Tools for Post-Processing Class Probability Estimates.” https://CRAN.R-project.org/package=probably.
Kuhn, Max, and Hadley Wickham. 2020. “Tidymodels: A Collection of Packages for Modeling and Machine Learning Using Tidyverse Principles.” https://www.tidymodels.org.
Pawley, Steven, Max Kuhn, and Rowan Jacques-Hamilton. 2023. “Colino: Recipes Steps for Supervised Filter-Based Feature Selection.” https://stevenpawley.github.io/colino.
Rosenberg, Daniel. 2022. “Unbalanced Data? Stop Using ROC-AUC and Use AUPRC Instead.” 2022. https://towardsdatascience.com/imbalanced-data-stop-using-roc-auc-and-use-auprc-instead-46af4910a494.
Waring, Elin, Michael Quinn, Amelia McNamara, Eduardo Arino de la Rubia, Hao Zhu, and Shannon Ellis. 2022. “Skimr: Compact and Flexible Summaries of Data.” https://CRAN.R-project.org/package=skimr.
Wickham, Hadley, Mara Averick, Jennifer Bryan, Winston Chang, Lucy D’Agostino McGowan, Romain François, Garrett Grolemund, et al. 2019. “Welcome to the Tidyverse” 4: 1686. https://doi.org/10.21105/joss.01686.