Forecasting with {modeltime} - Part I

Gathering data

Time Series
Data Acquisition
Data Wrangling
Author

Arcenis Rojas

Published

February 12, 2024

Introduction

Monopoly houses on top of increasingly tall stacks of coins

Image by [Images Money](https://www.flickr.com/photos/59937401@N07/)

I learned about the modeltime (Dancho 2023) package – developed by the folks at Business Science – in 2021 and hadn’t had much chance to use it except for a few small coding exercises. With U.S. housing prices have being all over the news in recent times I thought about trying to forecast a housing price metric. My curiosity about housing price trends presented the perfect opportunity to take on a small project using modeltime. My goal for this project will be to model multiple time series together using various algorithms through a global modeling process then select the best models from that process and use those algorithms to run an iterative modeling process on the time series to try to get the best forecasts.

I’ve broken this project into five parts:

  1. Gathering Data

  2. Time series analysis

  3. ARIMA with global and iterative modeling processes

  4. Global forecasting models

  5. Iterative forecasting models

This post will cover the first part: Gathering Data.

Choosing house price data

To perform this analysis, obviously the first thing I would need is a data set. I wanted data that had sufficient observations with enough granularity to be able to identify seasonality and level changes. I also wanted to compare time series across different regions or cities of the U.S. This meant getting data that was available at a regional/metropolitan level that went back at least 10 years with very few missing values (ideally none). I looked at the data available through the Federal Reserve Bank of St. Louis which hosts one of the largest repositories of U.S. economic data available by using the fredr (Boysel and Vaughan 2021) package and narrowed my search for data series down to either median home prices or the Case-Shiller Home Price Index. I chose the Case-Shiller HPI because I could get the data at the level of metro area rather than just U.S. region for a longer period of time, though there is the trade-off that this index only accounts for existing home sales. For my purposes this wasn’t a problem.

The Case-Shiller HPI data was available through 2023, but population data (discussed below) was available only through 2022 and there were some other issues with data from before 2006, so I got data starting in January 2006 and ending in December 2022.

Once I chose a data source, the next step was to choose cities. I wanted to compare cities from different regions of the U.S. that were different in other characteristics as well, e.g., population, climate, etc., to see how forecasts might differ. I chose San Diego, Dallas, Detroit, and New York City.

Additional data

One of the benefits of using modeltime it has functions for running models beyond ARIMA such as Prophet and eXtreme Gradient Boosting (XGB) for time series. To take advantage of this I wanted to add some features to my data. I chose to add unemployment rates, average gas prices, variables relating to demographic composition, and population for each city at the monthly level. I got the unemployment rate and average gas prices through fredr, population data from the U.S. Census’s American Community Survey (ACS) using the tidycensus (Walker and Herman 2024) package, and other demographic data from the Current Population Survey (CPS) (which is a joint program of the U.S. Census and the U.S. Bureau of Labor Statistics) using the cpsR (Saenz 2023) package.

Important

Both tidycensus and cpsR require a U.S. Census API key. This post will not go into detail on how to obtain a key or how to set it up for use with the relevant packages.

Some of these data are at the metropolitan statistical area (MSA) level and others are at the core-based statistical area (CBSA) level. While these broadly overlap, which is why I didn’t make a big fuss about mixing them, they are technically different. The U.S. Census provides some definitions here.

As usual for me, I performed data importing and wrangling using various tidyverse (Wickham et al. 2019)package functions. I also used multidplyr (Wickham 2023) to perform some operations in parallel.

Loading Packages

To begin with, I first loaded my packages. I’ll include the gt package for displaying tables.

Code 
library(tidyverse)
library(fredr)
library(tidycensus)
library(cpsR)
library(gt)
library(multidplyr)

conflicted::conflict_prefer("filter", "dplyr")
conflicted::conflict_prefer("lag", "dplyr")
conflicted::conflict_prefer("between", "dplyr")

Getting Case-Shiller HPI data

I started by getting the appropriate Case-Shiller HPI series IDs for my cities of interest.

Code 
hpi_ids <- fredr_series_search_text("Case-Shiller") |>
  filter(
    str_detect(
      title,
      "CA-San Diego|TX-Dallas|NY-New York|MI-Detroit Home Price Index"
    ),
    seasonal_adjustment_short %in% "NSA",
    frequency %in% "Monthly"
  ) |>
  mutate(city = str_extract(title, "New York|Dallas|San Diego|Detroit")) |>
  select(city, id)

gt(hpi_ids) |> gt_bold_head()
city id
San Diego SDXRNSA
Dallas DAXRNSA
New York NYXRNSA
Detroit DEXRNSA

Next I read in the Case-Shiller data and kept only the necessary variables.

Code 
hpi_data <- hpi_ids |>
  mutate(
    data = map(
      id,
      \(x) fredr(
        series_id = x,
        observation_start = ymd("2006-01-01"),
        observation_end = ymd("2023-12-31"),
        frequency = "m"
      )
    )
  ) |>
  select(-id) |>
  unnest(data) |>
  select(city, date, hpi = value)

hpi_data[1:10, ] |> gt() |> gt_bold_head()
city date hpi
Dallas 2006-01-01 121.9108
Dallas 2006-02-01 121.3285
Dallas 2006-03-01 121.5217
Dallas 2006-04-01 122.3996
Dallas 2006-05-01 123.2863
Dallas 2006-06-01 124.4985
Dallas 2006-07-01 125.3672
Dallas 2006-08-01 125.7007
Dallas 2006-09-01 125.1859
Dallas 2006-10-01 124.5813

Getting unemployment rate and gas price data from FRED

Next I got series IDs for both average gas prices and unemployment rates for all four cities and got the data for the appropriate time span.

Code 
# Get average gas price for each CBSA by month
gas_ids <- fredr_series_search_text(
  "Average Price: Gasoline, Unleaded Regular"
) |>
  filter(
    str_detect(title, "New York|Dallas|San Diego|Detroit"),
    frequency %in% "Monthly",
    seasonal_adjustment_short %in% "NSA"
  ) |>
  mutate(city = str_extract(title, "New York|Dallas|San Diego|Detroit")) |>
  select(city, id)

gas_data <- gas_ids |>
  mutate(
    data = map(
      id,
      \(x) fredr(
        series_id = x,
        observation_start = ymd("2000-01-01"),
        observation_end = ymd("2023-12-31"),
        frequency = "m"
      )
    )
  ) |>
  select(-id) |>
  unnest(data) |>
  select(city, date, avg_gas_price = value)

# Get average unemployment rate for each MSA by month
unemp_ids <- fredr_series_search_text("Unemployment: Rate") |>
  filter(
    str_detect(title, "New York|Dallas|San Diego|Detroit"),
    frequency %in% "Monthly",
    seasonal_adjustment_short %in% "NSA"
  ) |>
  mutate(city = str_extract(title, "New York|Dallas|San Diego|Detroit")) |>
  group_by(city) |>
  mutate(
    rnum = n(),
    msa_str = str_detect(title, "MSA")
  ) |>
  ungroup() |>
  filter(rnum == 1 | msa_str) |>
  select(city, id)

unemp_data <- unemp_ids |>
  mutate(
    data = map(
      id,
      \(x) fredr(
        series_id = x,
        observation_start = ymd("2000-01-01"),
        observation_end = ymd("2023-12-31"),
        frequency = "m"
      )
    )
  ) |>
  select(-id) |>
  unnest(data) |>
  select(city, date, unemp_rate = value)

Getting CPS data

Getting CPS data at the MSA level is a little more complicated than it is getting data series from FRED. CPS data can contain well over 100K rows for each month because the microdata are released at the household level and each data set has hundreds of variables. It also requires filtering and grouping the data by MSA code, which means getting the MSA codes that correspond to each MSA in my analysis. However, I knew that MSAs can change over time as population shifts. I felt confident that this wouldn’t be the case for my chosen cities because of their population sizes, but I wanted to check anyway. Finally, I did thought that pulling in all of that data at once then filtering and aggregating would be computationally inefficient and slow, so, instead, I wrote a function to perform all of the necessary operations and ran it in parallel. I chose the method that I did because most of the time was spent connecting to the CPS API. Once data are imported, the computations are fairly simple.

The first step was to get the MSA codes that corresponded to my cities of interest and check that I had a unique set across all of my years of interest. The data for these MSA codes came from the U.S. Census’s technical documentation page and MSA definitions only change once every few years.

Code 
msa_code_tbl <- tribble(
  ~start_yr, ~end_yr,
  2003, 2006,
  2007, 2011,
  2012, 2016,
  2017, 2021
) |>
  mutate(
    suffix = str_sub(start_yr, 3, 4),
    msa_url = map_chr(
      suffix,
      \(x) str_c(
        "https://www2.census.gov/programs-surveys/cbp/technical-documentation/",
        "reference/metro-area-geography-reference/msa_county_reference",
        x,
        ".txt"
      )
    ),
    msa_code_data = map(
      msa_url,
      \(x) read_delim(x, delim = ",", show_col_types = FALSE) |>
        filter(
          str_detect(
            name_msa,
            "Dallas.*TX|San Diego.*CA|New York.*NY|Detroit.*MI"
          )
        ) |>
        mutate(
          city = str_extract(name_msa, "Dallas|New York|San Diego|Detroit"),
          msa = as.character(msa)
        ) |>
        distinct(city, msa)
    )
  ) |>
  distinct(msa_code_data) |>
  unnest(msa_code_data)

msa_code_tbl |> gt() |> gt_bold_head()
city msa
Dallas 19100
Detroit 19820
New York 35620
San Diego 41740

In the next step I defined the function for importing, filtering, and aggregating CPS data.

Code 
get_cps_summaries <- function(cps_df, geographies) {
  cps_df |>
    rename(hispanic = matches("hspnon"), msa = starts_with("gt")) |>
    filter(msa %in% geographies) |>
    relocate(msa, pwsswgt, prtage, pemaritl, peeduca, hispanic) |>
    mutate(
      msa = as.character(msa),
      pwsswgt = as.numeric(pwsswgt),
      across(prtage:hispanic, as.integer),
      across(prtage:hispanic, \(x) na_if(x, -1)),
      age_lt_18 = prtage < 18,
      age_18_35 = between(prtage, 18, 35),
      age_36_65 = between(prtage, 36, 65),
      age_gt_65 = prtage > 65,
      educ_hs_less = peeduca < 40,
      educ_college = peeduca %in% 40:43,
      educ_grad = peeduca > 43,
      status_married = pemaritl %in% 1:2,
      status_nev_mar = pemaritl == 6,
      status_other = !pemaritl %in% c(1:2, 6),
      hispanic = hispanic == 1,
      across(
        c(age_lt_18:status_other, hispanic),
        \(x) (x * pwsswgt)
      )
    ) |>
    group_by(msa) |>
    summarise(
      across(
        c(age_lt_18:status_other, hispanic),
        \(x) sum(x / sum(pwsswgt), na.rm = TRUE)
      )
    )
}

With that function now defined, I move on to get CPS data using that function.

Code 
# Set up a cluster to get all of the CPS data aggregations
cps_clust <- new_cluster(12)
cluster_library(cps_clust, c("tidyverse", "cpsR"))
cluster_copy(cps_clust, c("get_cps_summaries", "msa_code_tbl"))

# Get CPS data aggregations
cps_grid <- expand.grid(
  yr = 2006:2023,
  mo = 1:12
) |>
  partition(cps_clust)

cps_data <- cps_grid |>
  arrange(yr, mo) |>
  mutate(
    cps = map2(
      yr, mo,
      possibly(
        \(y, m) {
          get_basic(
            y, m,
            c("gtcbsa", "prtage", "pemaritl", "peeduca", "pehspnon", "pwsswgt")
          ) |>
            get_cps_summaries(msa_code_tbl$msa)
        }
      )
    )
  ) |>
  collect() |>
  unnest(cps) |>
  mutate(msa = as.character(msa)) |>
  left_join(msa_code_tbl, by = "msa") |>
  select(-msa) |>
  unite("date", yr, mo, sep = "-") |>
  mutate(date = ym(date)) |>
  relocate(city, date)

This is what the CPS data looked like.

Code 
head(cps_data) |> gt() |> gt_bold_head()
city date age_lt_18 age_18_35 age_36_65 age_gt_65 educ_hs_less educ_college educ_grad status_married status_nev_mar status_other hispanic
Dallas 2006-01-01 0.2839770 0.2751600 0.3507462 0.08780246 0.3612863 0.3246959 0.06969308 0.4193003 0.2093507 0.3713489 0.23589661
Detroit 2006-01-01 0.2633059 0.2178059 0.3914485 0.12411556 0.3647213 0.3357047 0.07179506 0.4001588 0.2336782 0.3661630 0.03352171
New York 2006-01-01 0.2420728 0.2408729 0.3889675 0.12649394 0.3721424 0.3287271 0.09625312 0.4060160 0.2625960 0.3313880 0.19769087
San Diego 2006-01-01 0.2398891 0.2393884 0.3969656 0.12375698 0.2819756 0.4378574 0.08594332 0.3991201 0.2550806 0.3457992 0.24626772
Dallas 2006-03-01 0.2991726 0.2852235 0.3324601 0.08314374 0.3481381 0.3412725 0.06266023 0.4069059 0.2147862 0.3783079 0.27328065
Detroit 2006-03-01 0.2660104 0.2155320 0.4070590 0.11139867 0.3738536 0.3548189 0.05050216 0.4191846 0.2244699 0.3563455 0.03402642

Getting population data

One would think that if any demographic data is simple to get, population data would be simple, right? I learned something different. I was interested in getting population data at a monthly level for each MSA of interest. I knew population was not counted monthly, but I thought I could get it from the CPS. In fact, one might notice that the code actually calls a population variable (pwsswgt ) to perform some calculations. The problem here was that at the MSA level population estimates varied in some cases by as much as 16%. While I I didn’t know if this was true or not I did believe (subjectively) that it was unlikely and I believed that CPS weights are not calibrated to MSAs. My understanding is that they are calibrated to the national and state levels. So, I thought a reasonable alternative would be to get data from the ACS 1-year survey and interpolate data from one year to the next. In fact, the reason that I started my time series in 2006 is that the ACS 1-year and 5-year survey data became available in 2005 and I needed one year before the time series for interpolation. However, there was wrinkle caused by COVID. The 1-year ACS was not released for 2020 because of understandable challenges with data collection. So, for 2020 I used ACS 5-year survey data. I started by getting all of the ACS 1-year data. Here again, I processed the data in parallel.

Code 
# Create a cluster for getting ACS data
acs_clust <- new_cluster(12)
cluster_library(acs_clust, c("tidyverse", "tidycensus"))

# Get ACS data for 2005 to 2019, 2021, and 2022
acs1_pop_data <- tibble(year = c(2005:2019, 2021:2022)) |>
  partition(acs_clust) |>
  mutate(
    pop_data = map(
      year,
      \(x) get_acs(
        year = x,
        variables = "B01001_001",
        geography = "cbsa",
        survey = "acs1",
        show_call = FALSE
      ) |>
        filter(str_detect(NAME, "New York|Dallas|San Diego|Detroit")) |>
        mutate(city = str_extract(NAME, "New York|Dallas|San Diego|Detroit")) |>
        select(city, population = estimate)
    )
  ) |>
  collect() |>
  unnest(pop_data) |>
  mutate(date = str_c(year, "12") |> ym(), .keep = "unused")

Next I got the data for 2020 and combined it with the ACS 1-year data. I performed interpolation using the ts_impute_vec() function from the timetk (Dancho and Vaughan 2023) package.

Code 
# Get data for 2020 separately since it wasn't available in the ACS 1-year
acs5_pop_data <- get_acs(
  year = 2020,
  variables = "B01001_001",
  geography = "cbsa",
  survey = "acs5",
  show_call = FALSE
) |>
  filter(str_detect(NAME, "New York|Dallas|San Diego|Detroit")) |>
  mutate(
    city = str_extract(NAME, "New York|Dallas|San Diego|Detroit"),
    date = rep(ym("2020-12"), 4),
  ) |>
  select(city, date, population = estimate)

# Put together all the ACS population data and interpolate between annual
# estimates
acs_pop_data <- expand_grid(
  yr = 2006:2022,
  mo = 1:12
) |>
  add_row(yr = 2005, mo = 12) |>
  expand_grid(city = c("New York", "Dallas", "San Diego", "Detroit")) |>
  unite(date, yr, mo, sep = "-", remove = TRUE) |>
  mutate(date = ym(date)) |>
  arrange(date, city) |>
  left_join(
    bind_rows(acs1_pop_data, acs5_pop_data),
    by = c("city", "date")
  ) |>
  group_by(city) |>
  arrange(date) |>
  mutate(
    population = timetk::ts_impute_vec(population, period = 1),
    pop_chg = (population / lag(population)) - 1
  ) |>
  drop_na(pop_chg) |>
  ungroup() |>
  select(!population)

head(acs_pop_data) |> gt() |> gt_bold_head()
date city pop_chg
2006-01-01 Dallas 0.0040551186
2006-01-01 Detroit 0.0007530958
2006-01-01 New York 0.0021226567
2006-01-01 San Diego 0.0034579867
2006-02-01 Dallas 0.0040387411
2006-02-01 Detroit 0.0007525290

Merge data and check

With all of the data gathered and each data set containing variables for city and date (monthly) along with at least one demographic or economic variable, they were ready to be merged.

Code 
econ_data <- list(hpi_data, unemp_data, gas_data, cps_data, acs_pop_data) |>
  reduce(inner_join, by = c("city", "date"))

It would be a mistake to ever think that there is no more cleaning that can be done, so I skimmed the data using the skimr() function from the skimr (Waring et al. 2022) package.

Code 
skimr::skim(econ_data)
Data summary
Name econ_data
Number of rows 816
Number of columns 17
_______________________
Column type frequency:
character 1
Date 1
numeric 15
________________________
Group variables None

Variable type: character

skim_variable n_missing complete_rate min max empty n_unique whitespace
city 0 1 6 9 0 4 0

Variable type: Date

skim_variable n_missing complete_rate min max median n_unique
date 0 1 2006-01-01 2022-12-01 2014-06-16 204

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
hpi 0 1.00 172.19 64.38 64.47 122.40 168.06 203.87 427.80 ▆▇▃▁▁
unemp_rate 0 1.00 6.50 2.93 2.80 4.20 5.60 8.30 23.90 ▇▃▁▁▁
avg_gas_price 144 0.82 2.95 0.76 1.36 2.38 2.84 3.48 6.29 ▅▇▅▁▁
age_lt_18 0 1.00 0.24 0.02 0.19 0.22 0.24 0.25 0.30 ▂▇▇▃▂
age_18_35 0 1.00 0.25 0.02 0.18 0.24 0.25 0.26 0.31 ▁▂▇▆▁
age_36_65 0 1.00 0.39 0.02 0.33 0.38 0.39 0.40 0.45 ▁▃▇▂▁
age_gt_65 0 1.00 0.12 0.03 0.07 0.11 0.12 0.14 0.22 ▃▇▆▁▁
educ_hs_less 0 1.00 0.33 0.03 0.24 0.31 0.33 0.35 0.40 ▁▃▇▇▃
educ_college 0 1.00 0.38 0.03 0.30 0.36 0.38 0.40 0.48 ▂▇▇▅▁
educ_grad 0 1.00 0.10 0.02 0.05 0.08 0.10 0.11 0.16 ▃▇▇▃▁
status_married 0 1.00 0.40 0.02 0.32 0.39 0.40 0.41 0.45 ▁▁▇▇▂
status_nev_mar 0 1.00 0.27 0.03 0.19 0.25 0.27 0.29 0.34 ▂▆▇▇▂
status_other 0 1.00 0.33 0.02 0.28 0.32 0.33 0.34 0.46 ▃▇▂▁▁
hispanic 0 1.00 0.22 0.11 0.02 0.17 0.25 0.30 0.42 ▅▁▆▇▂
pop_chg 0 1.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 ▁▂▇▃▁

Overall the data look good except for the avg_gas_price variable, which is the only variable that has any missing values. I’ll turn to that shortly, but I’ll briefly describe the variables in the data set below:

  • city : self-explanatory

  • date: month expressed as the first day of the month

  • hpi: Case-Shiller Home Price Index value

  • unemp_rate: Unemployment rate

  • avg_gas_price: Average gas price

  • age_lt_18: Proportion of the population younger than 18 years old

  • age_18_35: Proportion of the population between the ages of 18 and 35

  • age_36_65: Proportion of the population between the ages of 36 and 65

  • age_gt_65: Proportion of the population older than 65 years old

  • educ_hs_less: Proportion of the population with up to a high school diploma

  • educ_college: Proportion of the population with more than a high school diploma and up to a bachelor’s degree

  • educ_grad: Proportion of the population with education higher than a bachelor’s degree

  • status_married: Proportion of the population that is married; including separated

  • status_nev_mar: Proportion of the population that has never been married

  • status_other: Proportion of the population not categorized as either status_married or status_nev_mar

  • hispanic: Proportion of the population that reported Hispanic ethnicity

  • pop_chg: Population change from one month to the next

Once I skimmed the data, I took a closer look at the percent of avg_gas_price values that were missing for each city.

Code 
econ_data |>
  group_by(city) |>
  summarise(pct_miss_gas = sum(is.na(avg_gas_price)) / n()) |>
  ggplot(aes(y = pct_miss_gas, x = city)) +
  geom_col(fill = "#2c3e50") +
  scale_y_continuous(limits = c(-0.1, 1.1), labels = scales::percent) +
  labs(
    y = "Percent Missing",
    x = NULL,
    title = "Missingness in avg_gas_price variable by city"
  ) + 
  theme_bw() +
  theme(plot.title = element_text(hjust = 0.5))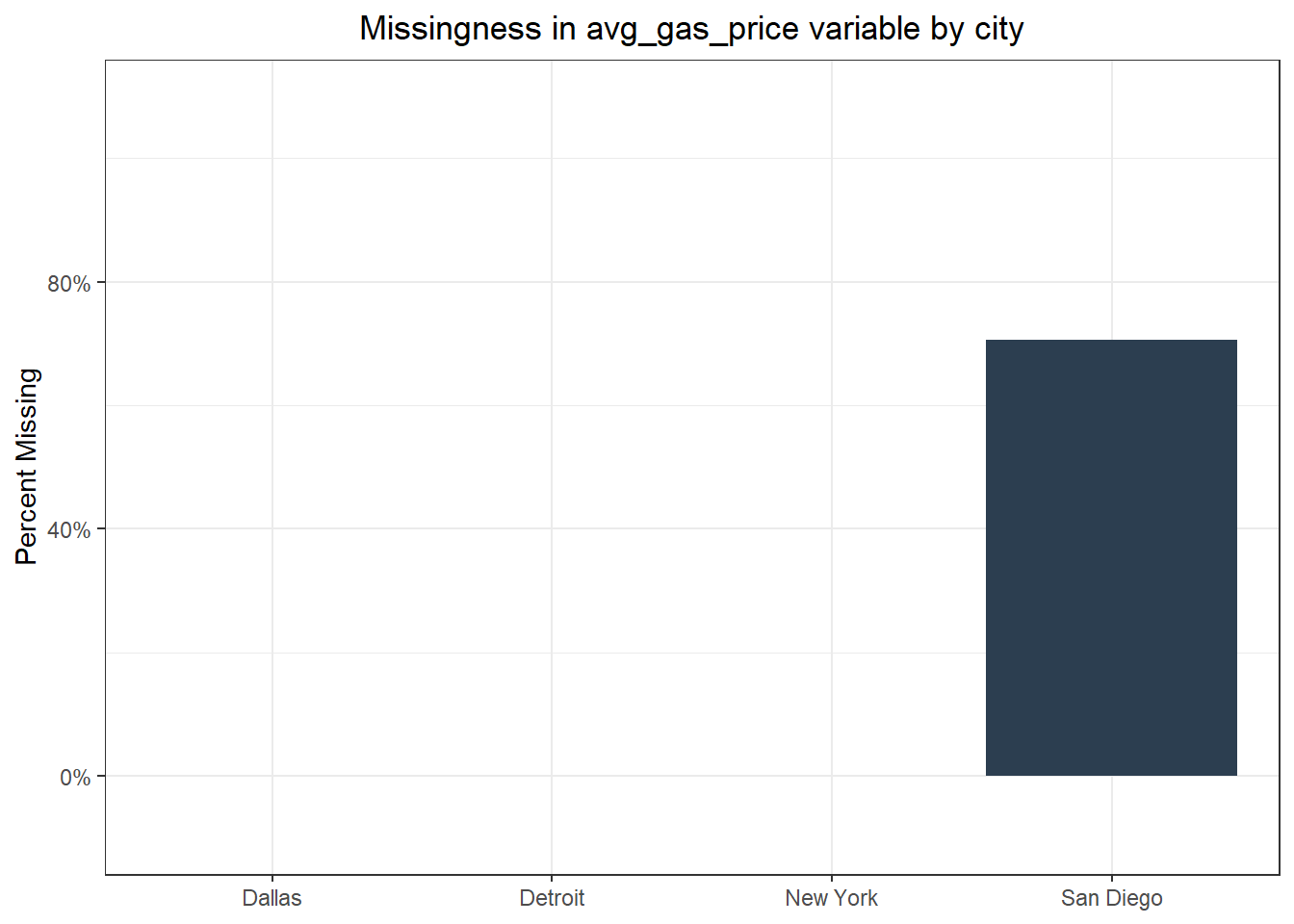

Evidently data were missing only for San Diego. Below are the start and end dates of average gas price data for San Diego in this data set.

Code 
econ_data |>
  filter(city %in% "San Diego", !is.na(avg_gas_price)) |>
  summarise(start_date = min(date), end_date = max(date)) |>
  gt() |>
  gt_bold_head()
start_date end_date
2018-01-01 2022-12-01

As it turns out, reports of average gas price data for San Diego start in January of 2018, which means that 12 years of data would be missing. With that many values missing for one of the cities it makes sense to drop the average gas price variable.

Code 
econ_data <- select(econ_data, !avg_gas_price)

econ_data |> slice(1:6) |> gt() |> gt_bold_head()
city date hpi unemp_rate age_lt_18 age_18_35 age_36_65 age_gt_65 educ_hs_less educ_college educ_grad status_married status_nev_mar status_other hispanic pop_chg
Dallas 2006-01-01 121.9108 5.1 0.2839770 0.2751600 0.3507462 0.08780246 0.3612863 0.3246959 0.06969308 0.4193003 0.2093507 0.3713489 0.2358966 0.004055119
Dallas 2006-02-01 121.3285 5.2 0.2955885 0.2749812 0.3499053 0.07952504 0.3534445 0.3474221 0.05914608 0.4186053 0.2195799 0.3618148 0.2640835 0.004038741
Dallas 2006-03-01 121.5217 5.0 0.2991726 0.2852235 0.3324601 0.08314374 0.3481381 0.3412725 0.06266023 0.4069059 0.2147862 0.3783079 0.2732806 0.004022495
Dallas 2006-04-01 122.3996 4.8 0.2938252 0.2784571 0.3445776 0.08314010 0.3324701 0.3589532 0.06155738 0.3932068 0.2133219 0.3934713 0.2540514 0.004006380
Dallas 2006-05-01 123.2863 4.9 0.2744636 0.2824573 0.3631222 0.07995692 0.3610289 0.3519889 0.05978182 0.4005990 0.2167855 0.3826155 0.2722199 0.003990393
Dallas 2006-06-01 124.4985 5.3 0.2739175 0.2861816 0.3643186 0.07558240 0.3512415 0.3512756 0.06253083 0.4065603 0.2122996 0.3811401 0.2734042 0.003974533

Finally, I’d like to visualize the densities of all of the variables by city just to make sure nothing jumps out that might need any correction.

Code 
econ_data |>
  select(-date) |>
  pivot_longer(-city, names_to = "variable") |>
  ggplot(aes(x = value, fill = city)) +
  geom_density(alpha = 0.5) +
  facet_wrap("variable", scales = "free") +
  theme_bw()

There are some interesting patterns, particularly in the differences across the age groups, but there’s nothing alarming. With all this data in hand, the next step is to perform some time series analysis on the Case-Shiller HPI which I’ll show in Part 2 of this set of posts.

References

Boysel, Sam, and Davis Vaughan. 2021. “Fredr: An r Client for the ’FRED’ API.” https://CRAN.R-project.org/package=fredr.
Dancho, Matt. 2023. “Modeltime: The Tidymodels Extension for Time Series Modeling.” https://CRAN.R-project.org/package=modeltime.
Dancho, Matt, and Davis Vaughan. 2023. “Timetk: A Tool Kit for Working with Time Series.” https://CRAN.R-project.org/package=timetk.
Saenz, Matt. 2023. “cpsR: Load CPS Microdata into r Using the ’Census Bureau Data’ API.” https://CRAN.R-project.org/package=cpsR.
Walker, Kyle, and Matt Herman. 2024. “Tidycensus: Load US Census Boundary and Attribute Data as ’Tidyverse’ and ’Sf’-Ready Data Frames.” https://CRAN.R-project.org/package=tidycensus.
Waring, Elin, Michael Quinn, Amelia McNamara, Eduardo Arino de la Rubia, Hao Zhu, and Shannon Ellis. 2022. “Skimr: Compact and Flexible Summaries of Data.” https://CRAN.R-project.org/package=skimr.
Wickham, Hadley. 2023. “Multidplyr: A Multi-Process ’Dplyr’ Backend.” https://CRAN.R-project.org/package=multidplyr.
Wickham, Hadley, Mara Averick, Jennifer Bryan, Winston Chang, Lucy D’Agostino McGowan, Romain François, Garrett Grolemund, et al. 2019. “Welcome to the Tidyverse” 4: 1686. https://doi.org/10.21105/joss.01686.