Forecasting with {modeltime} - Part IV

Tuning many global models

Time Series
Forecasting
Machine Learning
Author

Arcenis Rojas

Published

February 20, 2024

Review

Up to this point in the project I acquired data in Forecasting with {modeltime} - Part I, performed some standard time series analysis in Forecasting with {modeltime} - Part II, and explored the two types of modeling processes – global and iterative – for multiple time series in Forecasting with {modeltime} - Part III. In this post I’m going to tune multiple models using a global process to select a small number of them that I will run iteratively in the final post. I’ll incorporate some of the other variables in the data set that I gathered in the the first post to forecast the Case-Shiller Home Price Index (HPI). Since I’ll be creating variations of model specifications, I’m also going to use functions from the Tidymodels workflowsets (Kuhn and Couch 2023) package to run the models. As before I’ll be using modeltime (Dancho 2023), timetk (Dancho and Vaughan 2023), tidymodels (Kuhn and Wickham 2020), tidyverse (Wickham et al. 2019), and gt (Iannone et al. 2024). Before jumping in, below I show a glimpse of the data that I’ll be using.

Code 
library(tidyverse)
library(timetk)
library(modeltime)
library(tidymodels)
library(gt)
conflicted::conflict_prefer("filter", "dplyr")
conflicted::conflict_prefer("lag", "dplyr")
tidymodels_prefer()
Code 
skimr::skim(econ_data)
Data summary
Name econ_data
Number of rows 816
Number of columns 16
_______________________
Column type frequency:
character 1
Date 1
numeric 14
________________________
Group variables None

Variable type: character

skim_variable n_missing complete_rate min max empty n_unique whitespace
city 0 1 6 9 0 4 0

Variable type: Date

skim_variable n_missing complete_rate min max median n_unique
date 0 1 2006-01-01 2022-12-01 2014-06-16 204

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
hpi 0 1 172.19 64.38 64.47 122.40 168.06 203.87 427.80 ▆▇▃▁▁
unemp_rate 0 1 6.50 2.93 2.80 4.20 5.60 8.30 23.90 ▇▃▁▁▁
age_lt_18 0 1 0.24 0.02 0.19 0.22 0.24 0.25 0.30 ▂▇▇▅▂
age_18_35 0 1 0.25 0.02 0.20 0.24 0.25 0.26 0.31 ▁▃▇▃▁
age_36_65 0 1 0.39 0.02 0.33 0.38 0.39 0.40 0.44 ▁▃▇▂▁
age_gt_65 0 1 0.12 0.02 0.07 0.11 0.12 0.14 0.19 ▃▆▇▅▁
educ_hs_less 0 1 0.33 0.03 0.24 0.31 0.33 0.35 0.40 ▁▃▇▇▃
educ_college 0 1 0.38 0.03 0.31 0.36 0.38 0.40 0.48 ▂▇▆▃▁
educ_grad 0 1 0.10 0.02 0.05 0.08 0.10 0.11 0.16 ▃▇▇▅▁
status_married 0 1 0.40 0.02 0.32 0.39 0.40 0.41 0.45 ▁▁▇▇▂
status_nev_mar 0 1 0.27 0.03 0.19 0.25 0.27 0.29 0.34 ▂▅▇▇▂
status_other 0 1 0.33 0.02 0.28 0.32 0.33 0.34 0.45 ▃▇▃▁▁
hispanic 0 1 0.22 0.11 0.02 0.17 0.25 0.30 0.42 ▅▁▆▇▂
population 0 1 8471150.57 6499655.47 2834025.25 4050215.00 5109791.12 10555276.77 20320876.00 ▇▃▁▁▃

Splitting the data

The data split object for a global modeling process is different than that for an iterative modeling process. For the global modeling process I’ll use timetk::time_series_split() . Below is a look at how the data are split.

Code 
econ_splits <- econ_data |>
  time_series_split(
    assess = "2 year",
    cumulative = TRUE,
    date_var = date
  )

econ_splits
<Analysis/Assess/Total>
<720/96/816>

Choosing algorithms

As with selecting the cities in the analysis I’m interested in getting a little variation in the algorithms to see how they perform and I want to vary the parameters a bit. To get something of a traditional flavor I’m going to run ARIMA models with three different model formulas:

1) hpi ~ date

2) hpi ~ date + unemployment

3) hpi ~ date + unemployment + demographic variables

I’ll also have four specifications for the algorithms. One will be the default auto-ARIMA and the other three will be auto-ARIMA specifications with different season lengths. This will give me twelve different ARIMA models (3 recipes x 4 algorithm specifications).

In much the same way I will have different sets of recipes and model specifications for the following:

  • an exponential smoothing algorithm (including a Holt-Winters specification) to allow for weighting the periods exponentially

  • an STLM algorithm using an ARIMA engine (STLM: Seasonal Trend Decomposition using Loess with Multiple seasonal periods)

  • A feed-forward, auto-regressive neural-net algorithm because these tend to have high predictive ability

Some of these algorithms allow for covariates and others (like exponential smoothing) do not. In the end I will have 90 model specifications to test. In order to do speed up the processing I’ll employ modeltime’s parallel processing feature.

Building workflow objects

Here I’ll write the three recipes for the ARIMA models and one for the auto-regressive neural-net model. The exponential smoothing and STLM models will both use the first of the three ARIMA recipes as neither of these algorithms can handle covariates.

You might notice in the code below that I exclude some of the demographic variables like “educ_hs_less” for the third ARIMA recipe. I exclude these variables because I found that including all of the variables for a demographic variable group causes the functions to error out much in the same way that including all of the categories of a factor variable would. Initially I did not expect that I would need contrasts considering that the variable values are ratios, but it seems that the fact that the sum of the ratios for a given variable group, e.g., education, is 1 for each row and for each variable group creates a need for contrasts in the regression (this is my guess).

Writing recipes

Code Explanations

Some of the code chunks below contain explanations. Lines in explanations will be marked with encircled numbers. Just hover over those numbers to see the corresponding explanation.

Code 
arima_rec1 <- recipe(hpi ~ date, data = training(econ_splits))

arima_rec2 <- recipe(
  hpi ~ date + unemp_rate,
  data = training(econ_splits)
) |>
  step_center(all_numeric_predictors()) |>
  step_scale(all_numeric_predictors()) |>
  step_lag(unemp_rate, lag = c(1, 3, 6))

rec3_dep_vars <- econ_data |>
  select(date, unemp_rate:population) |>
  select(!c(educ_hs_less, status_married, age_36_65)) |>
  names() |>
  str_flatten(collapse = " + ")

arima_rec3 <- recipe(
  formula(str_c("hpi", rec3_dep_vars, sep = " ~ ")),
  data = training(econ_splits)
) |>
  step_center(all_numeric_predictors()) |>
  step_scale(all_numeric_predictors()) |>
  step_lag(unemp_rate, population, lag = c(1, 3, 6))

nnet_rec <- recipe(
  hpi ~ .,
  data = training(econ_splits)
) |>
  update_role(city, new_role = "ID") |>
  step_center(all_numeric_predictors()) |>
  step_scale(all_numeric_predictors()) |>
  step_timeseries_signature(date) |>
  step_nzv(all_predictors())
1
Write a base recipe to regress HPI on the date variable
2
Write a recipe formula that adds unemployment as an explanatory variable
3
Mean-center all numeric predictors (only “unemployment rate” here)
4
Scale all numeric predictors to have a mean of “0” and a standard error of 1
5
Create lag variables for “unemployment rate” and “population”
6
Get the names of all the economic and demographic variables from the data set and concatenate them into a formula string to make the right side of a regression formula, i.e., “var1 + var2 + var3…”
7
Because the “outcome ~ .” notation is being used, the “city” variable is included in the “.”, meaning it will be treated as an explanatory variable. This step changes the role of that variable from “predictor” to an ID variable, which modeling workflows will exclude from sets of predictors.
8
Add a set of variables related to the date such as day of the week of the date, day of the month, number of the week of the year, etc.
9
Remove any variables with zero or near-zero variance. An example of this would be a variable indicating the day of the month. Since this is monthly data, all values would be “1”, i.e., the first day of the month.

Here is a reminder of what a recipe looks like. This is the neural-net recipe.

Code 
nnet_rec

And this is the data set that gets created by that recipe.

Code 
nnet_rec |> prep() |> juice() |> slice(1:5) |> gt() |> gt_bold_head()
city date unemp_rate age_lt_18 age_18_35 age_36_65 age_gt_65 educ_hs_less educ_college educ_grad status_married status_nev_mar status_other hispanic population hpi date_index.num date_year date_year.iso date_half date_quarter date_month date_month.xts date_month.lbl date_wday date_wday.xts date_wday.lbl date_qday date_yday date_mweek date_week date_week.iso date_week2 date_week3 date_week4
Dallas 2006-01-01 -0.5318986 1.9837898 1.2244300 -2.1179446 -1.4144536 1.4132488 -1.9352723 -1.0007519 0.7138177 -1.8445270 1.9655339 0.2421831 -0.4128166 121.9108 1136073600 2006 2005 1 1 1 0 January 1 0 Sunday 1 1 5 1 52 1 1 1
San Diego 2006-01-01 -0.8651452 -0.2639636 -0.5419655 -0.1248023 0.7104276 -0.6271533 1.1018075 -0.5165046 -0.8376538 -0.5633246 1.4600357 0.4759810 -0.8614678 247.4588 1136073600 2006 2005 1 1 1 0 January 1 0 Sunday 1 1 5 1 52 1 1 1
New York 2006-01-01 -0.5652232 0.4335013 -0.7101494 -0.3141128 0.2439870 1.6923074 -1.9655377 0.3044405 -0.5241964 -0.2666740 0.7951381 -0.1053321 1.5314733 213.4958 1136073600 2006 2005 1 1 1 0 January 1 0 Sunday 1 1 5 1 52 1 1 1
Detroit 2006-01-01 0.1679193 1.1233044 -1.7256753 -0.3452176 0.4389330 1.7816712 -1.6797175 -1.2833046 -0.7472264 -1.1655961 2.2179937 -1.6335110 -0.6156132 126.6627 1136073600 2006 2005 1 1 1 0 January 1 0 Sunday 1 1 5 1 52 1 1 1
Dallas 2006-02-01 -0.4985739 2.4431155 1.3332951 -2.2373194 -1.7310508 0.7705532 -0.9746432 -1.6783801 1.0008565 -1.5342766 1.3033739 0.4153678 -0.4092439 121.3285 1138752000 2006 2006 1 1 2 1 February 4 3 Wednesday 32 32 5 5 5 1 2 1

Specifying models

In this next step I’ll specify the model objects for each algorithm along with the search grids for their various hyperparameters. I chose to keep only some of the combinations of the exponential smoothing specifications to limit the number of models being run that are likely to fail.

Code 
arima_default <- arima_reg() |> set_engine("auto_arima")

arima_spec_grid <- tibble(seasonal_period = seq(9, 18, by = 3)) |>
  create_model_grid(
    f_model_spec = arima_reg,
    engine_name = "auto_arima",
    mode = "regression"
  )

ets_default <- exp_smoothing() |> set_engine("ets")

set.seed(40)
alpha_vals <- runif(5, 0.01, 0.5) *
  sample(c(1, 0.1, 0.01, .001), 5, replace = TRUE)
beta_vals <- runif(5, 0.01, 0.2) * sample(c(1, 0.1, 0.01), 5, replace = TRUE)
gamma_vals <- map_dbl(
  alpha_vals,
  \(x) runif(1, 0, 1 - x)
)

ets_spec_grid <- expand_grid(
  smooth_level = alpha_vals[-2],
  smooth_seasonal = gamma_vals[2:3],
  seasonal_period = seq(9, 18, by = 3)
) |>
  create_model_grid(
    f_model_spec = exp_smoothing,
    engine_name = "ets",
    mode = "regression",
    error = "auto",
    trend = "auto",
    season = "auto",
    smooth_trend = beta_vals[3]
  )

stlm_spec_grid <- expand_grid(
  seasonal_period_2 = c(NULL, seq(6, 18, by = 3))
) |>
  create_model_grid(
    f_model_spec = seasonal_reg,
    engine_name = "stlm_arima",
    mode = "regression",
    seasonal_period_1 = 12
  )

nnet_default <- nnetar_reg() |> set_engine("nnetar")

nnet_spec_grid <- expand_grid(
  non_seasonal_ar = 1:3,
  hidden_units = 3:5,
  num_networks = c(20, 25),
  penalty = c(0.2, 0.25)
) |>
  create_model_grid(
    f_model_spec = nnetar_reg,
    engine_name = "nnetar",
    mode = "regression",
    seasonal_period = 12,
    epochs = 100,
    seasonal_ar = 1
  )
1
Specify an ARIMA regression model using the “auto_arima” engine with all default arguments
2
Create a 1-column tibble (data frame) with the seasonal_period argument set to vary as 9, 12, 15, and 18 (months).
3
create_model_grid() allows one to set static arguments to combine them with the arguments that vary. This is meant to serve a similar purpose as tune::tune_grid() from Tidymodels.
4
Set a random seed for reproducibility and generate vectors for the smooth_level, smooth_trend, and smooth_seasonal arguments. In forecast::ets() these are alpha, beta, and gamma respectively.
5
Use tidyr::expand_grid() to get all combinations of the included vectors.

Below is what a model grid looks like.

Code 
ets_spec_grid |> slice(1:5)
# A tibble: 5 × 4
  smooth_level smooth_seasonal seasonal_period .models  
         <dbl>           <dbl>           <dbl> <list>   
1       0.0345           0.569               9 <spec[+]>
2       0.0345           0.569              12 <spec[+]>
3       0.0345           0.569              15 <spec[+]>
4       0.0345           0.569              18 <spec[+]>
5       0.0345           0.763               9 <spec[+]>

This is a glimpse of a model specification.

Code 
ets_spec_grid |> slice(1) |> pluck(".models", 1)
Exponential Smoothing State Space Model Specification (regression)

Main Arguments:
  seasonal_period = 9
  error = auto
  trend = auto
  season = auto
  smooth_level = 0.0344955188313033
  smooth_trend = 0.0247416579537094
  smooth_seasonal = 0.569256213388705

Computational engine: ets

Building workflowsets

A workflowset is, you guessed it, a set of workflows. Mechanically it is a very convenient wrapper that can put together different combinations of recipes (pre-processors) and models. I don’t want to mix all of my recipes with all of my models, however. So, in this step I’ll make sets of individuals that combine the appropriate sets of recipes and models then I’ll bind all of them together at the end.

Code 
arima_wfset <- workflow_set(
  preproc = list(
    base_rec = arima_rec1,
    econ_rec = arima_rec2,
    demog_rec = arima_rec3
  ),
  models = c(
    arima_default = list(arima_default),
    arima_spec = arima_spec_grid$.models
  ),
  cross = TRUE
)

ets_wfset <- workflow_set(
  preproc = list(base_rec = arima_rec1),
  models = c(ets_default = list(ets_default), ets_spec = ets_spec_grid$.models),
  cross = TRUE
)

stlm_wfset <- workflow_set(
  preproc = list(base_rec = arima_rec1),
  models = c(stlm_spec = stlm_spec_grid$.models),
  cross = TRUE
)

nnet_wfset <- workflow_set(
  preproc = list(nnet_rec = nnet_rec),
  models = c(
    nnet_default = list(nnet_default),
    nnet_spec = nnet_spec_grid$.models
  ),
  cross = TRUE
)
1
Call workflowsets::workflowset()
2
Provide a named list of recipes to use in the workflowset; naming the elements at this stage makes it easier to match up the elements of the final table containing the trained models with the original recipes and model specifications
3
Provide a named list of model specifications by pulling the “.models” column from each grid
4
Indicate that all recipes should be combined with all model specifications

The individual specifications in the final model table will be named using a combination of the name of the recipe and the name of the model specification given in the respective lists with a count added whenever there are duplicate names. For example, arima_spec_grid has four model specifications in it. The ones that are combined with the first ARIMA recipe (named “base_rec”) will be named BASE_REC_ARIMA_SPEC1, BASE_REC_ARIMA_SPEC2, BASE_REC_ARIMA_SPEC3, and BASE_REC_ARIMA_SPEC4.

With all of the model-specific workflow sets created, now it’s time to put them all together.

Code 
hpi_wfset <- bind_rows(arima_wfset, ets_wfset, stlm_wfset, nnet_wfset)

hpi_wfset |> slice(1:5)
# A workflow set/tibble: 5 × 4
  wflow_id               info             option    result    
  <chr>                  <list>           <list>    <list>    
1 base_rec_arima_default <tibble [1 × 4]> <opts[0]> <list [0]>
2 base_rec_arima_spec1   <tibble [1 × 4]> <opts[0]> <list [0]>
3 base_rec_arima_spec2   <tibble [1 × 4]> <opts[0]> <list [0]>
4 base_rec_arima_spec3   <tibble [1 × 4]> <opts[0]> <list [0]>
5 base_rec_arima_spec4   <tibble [1 × 4]> <opts[0]> <list [0]>

That’s all the heavy lifting. Now it’s time to let the computer processors do their part and run the models.

Fitting the models

Code 
avail_cores <- unname(parallelly::availableCores() - 1)
modulo_vec <- sapply(avail_cores:2, \(x) nrow(hpi_wfset) %% x)
           
num_cores <- max(
  max(which(modulo_vec == max(modulo_vec))),
    max(which(modulo_vec == 0))
) + 1

cl <- parallel::makePSOCKcluster(num_cores)
doParallel::registerDoParallel(cl)
invisible(
  parallel::clusterCall(cl, function(x) .libPaths(x), .libPaths())
)
invisible(parallel::clusterEvalQ(cl, set.seed(500)))

hpi_mods_start <- proc.time()

hpi_mods <- hpi_wfset |>
  modeltime_fit_workflowset(
    data = training(econ_splits),
    control = control_fit_workflowset(verbose = FALSE, allow_par = TRUE)
  )

hpi_mods_end <- proc.time()

parallel::stopCluster(cl)
rm(cl)
1
Get the number of cores available and leave one out for common tasks like running the operating system
2
Calculate the number of cores to use in order to maximize efficiency
3
Set up the cluster for parallel processing; I copied this code from modeltime::parallel_start()
4
Set the same random seed for each node
5
Call the workflowset object containing all the workflows to run
6
Use modeltime::modeltime_fit_workflowset() to fit all of the models
7
Use the training portion of the split object to train the models
8
Set some controls for the model fitting function
9
Stop the parallel cluster from running
Code 
hpi_mods |> as_tibble()
# A tibble: 90 × 3
   .model_id .model     .model_desc           
       <int> <list>     <chr>                 
 1         1 <workflow> BASE_REC_ARIMA_DEFAULT
 2         2 <workflow> BASE_REC_ARIMA_SPEC1  
 3         3 <workflow> BASE_REC_ARIMA_SPEC2  
 4         4 <workflow> BASE_REC_ARIMA_SPEC3  
 5         5 <workflow> BASE_REC_ARIMA_SPEC4  
 6         6 <workflow> ECON_REC_ARIMA_DEFAULT
 7         7 <workflow> ECON_REC_ARIMA_SPEC1  
 8         8 <workflow> ECON_REC_ARIMA_SPEC2  
 9         9 <workflow> ECON_REC_ARIMA_SPEC3  
10        10 <workflow> ECON_REC_ARIMA_SPEC4  
# ℹ 80 more rows
Code 
fit_time <- (hpi_mods_end - hpi_mods_start) |>
  enframe("time_metric", "seconds") |>
  drop_na(seconds)

fit_time |> gt() |> gt_bold_head()
time_metric seconds
user.self 1.48
sys.self 0.26
elapsed 83.06

About 83.06 seconds elapsed during model-fitting with parallel processing. Not too bad. Unfortunately, though, some of the models failed (I suppressed error printing). So, before calibrating the models I’m going to drop those from the model output data set. But first I’ll investigate the model failures a little.

Investigating failed models

Here’s a look at some of the models that failed.

Code 
mod_fail_df <- hpi_mods |>
  mutate(mod_fail = map_lgl(.model, \(x) is.null(x))) |>
  select(!.model)

mod_fail_df |>
  group_by(mod_fail) |>
  slice_min(.model_id, n = 3) |>
  gt(groupname_col = NULL) |>
  gt_bold_head()
.model_id .model_desc mod_fail
1 BASE_REC_ARIMA_DEFAULT FALSE
2 BASE_REC_ARIMA_SPEC1 FALSE
3 BASE_REC_ARIMA_SPEC2 FALSE
33 BASE_REC_ETS_SPEC17 TRUE
34 BASE_REC_ETS_SPEC18 TRUE
35 BASE_REC_ETS_SPEC19 TRUE

Now I want to see the distinct names of the recipes and algorithms (model specifications) that failed.

Code 
failure_spec_df <- mod_fail_df |>
  filter(mod_fail) |>
  separate_wider_delim(
    .model_desc,
    delim = "_",
    names = c("rec_name", "rec", "algo", "spec")
  ) |>
  separate_wider_regex(spec, patterns = c(spec = "SPEC", spec_num = "\\d+"))

failure_spec_df |> distinct(rec_name, algo, spec) |> gt() |> gt_bold_head()
rec_name algo spec
BASE ETS SPEC

Since the failures occurred with only one algorithm they’ll be easy to isolate. Now I want to get the numbers of the specifications that failed so that I can pull up the details on those specifications.

Code 
failures <- failure_spec_df |>
  pull(spec_num) |>
  as.numeric()

ets_failed <- ets_spec_grid |>
  slice(failures) |>
  select(!.models)

ets_failed |>
  count(smooth_level) |>
  gt() |>
  gt_bold_head()
smooth_level n
6.680868e-05 8

Overall there were 8 out of 32 failed exponential smoothing models. That’s not terrible. I’m going to remove these specifications from the trained model data set and move on to model evaluation.

Model evaluation

To evaluate the models first I need to calibrate them. I’ll remove the failed models, calibrate the successful ones, and store accuracy tables here. Below are the 10 best-performing global models, i.e., the ones that performed best on the batched series with all four cities. I defined “best” as the models with the lowest SMAPE (Scaled Mean Average Percent Error) values.

I broke up the code for calibrating the models below into two separate chunks to keep the file sizes of cached files a bit smaller. I cached the output to make the page easier to render. This step of splitting up the modeltime_table for calibration is not typically necessary.

Code 
hpi_mods <- hpi_mods |> slice(which(!mod_fail_df$mod_fail))

num_mods <- nrow(hpi_mods)
hpi_mod_idx <- split(1:num_mods, ceiling(seq_along(1:num_mods) / (num_mods / 3)))
Code 
hpi_mod_calib1 <- hpi_mods |>
  slice(hpi_mod_idx[[1]]) |>
  modeltime_calibrate(testing(econ_splits), id = "city", quiet = TRUE)
Code 
hpi_mod_calib2 <- hpi_mods |>
  slice(hpi_mod_idx[[2]]) |>
  modeltime_calibrate(testing(econ_splits), id = "city", quiet = TRUE)
Code 
hpi_mod_calib3 <- hpi_mods |>
  slice(hpi_mod_idx[[3]]) |>
  modeltime_calibrate(testing(econ_splits), id = "city", quiet = TRUE)
Code 
hpi_mod_calib <- bind_rows(hpi_mod_calib1, hpi_mod_calib2, hpi_mod_calib3)
Code 
hpi_mod_accuracy <- hpi_mod_calib |>
  modeltime_accuracy() |>
  drop_na(.type)

hpi_local_mod_accuracy <- hpi_mod_calib |>
  modeltime_accuracy(acc_by_id = TRUE) |>
  drop_na(.type)

best_global_table <- hpi_mod_accuracy |>
  slice_min(smape, n = 10)

best_local_table <- hpi_local_mod_accuracy |>
  group_by(city) |>
  slice_min(smape, n = 3)

best_global_table |>
  table_modeltime_accuracy(
    .interactive = FALSE,
    .title = "Global Accuracy"
  ) |>
  gt_bold_head() |>
  tab_style(
    style = cell_text(weight = "bold"),
    locations = cells_title()
  )
Global Accuracy
.model_id .model_desc .type mae mape mase smape rmse rsq
16 BASE_REC_ETS_DEFAULT Test 19.29 6.22 0.18 6.59 28.08 0.96
1 BASE_REC_ARIMA_DEFAULT Test 20.79 7.14 0.19 7.37 29.50 0.95
3 BASE_REC_ARIMA_SPEC2 Test 20.79 7.14 0.19 7.37 29.50 0.95
30 BASE_REC_ETS_SPEC14 Test 20.81 7.48 0.19 7.60 28.89 0.95
22 BASE_REC_ETS_SPEC6 Test 20.80 7.48 0.19 7.60 28.87 0.95
46 BASE_REC_ETS_SPEC30 Test 22.16 7.53 0.21 7.82 31.18 0.95
42 BASE_REC_ETS_SPEC26 Test 22.31 7.77 0.21 8.00 31.01 0.95
53 BASE_REC_STLM_SPEC5 Test 30.98 9.75 0.29 10.59 43.56 0.94
49 BASE_REC_STLM_SPEC1 Test 31.20 9.81 0.29 10.68 43.87 0.93
52 BASE_REC_STLM_SPEC4 Test 32.10 10.02 0.30 10.94 45.27 0.93

Next is a table with the best 3 models calibrated to each city.

Code 
best_local_table|>
  table_modeltime_accuracy(
    .interactive = FALSE,
    .title = "Accuracy by City"
  ) |>
  gt_bold_head() |>
  tab_style(
    style = cell_text(weight = "bold"),
    locations = cells_title()
  ) |>
  tab_style(
    style = list(cell_text(weight = "bold"), cell_fill(color = "lightgray")),
    locations = cells_group()
  ) |>
  tab_style(
    style = cell_borders(
      sides = c("top", "bottom"),
      weight = px(2),
      style = ("solid")
    ),
    locations = cells_group()
  )
Accuracy by City
.model_id .model_desc .type mae mape mase smape rmse rsq
Dallas
12 DEMOG_REC_ARIMA_SPEC1 Test 13.99 5.18 2.65 5.32 15.79 0.80
14 DEMOG_REC_ARIMA_SPEC3 Test 14.19 5.24 2.69 5.39 15.97 0.80
22 BASE_REC_ETS_SPEC6 Test 20.59 7.34 3.93 7.72 24.76 0.85
Detroit
76 NNET_REC_NNET_SPEC22 Test 2.73 1.64 1.55 1.65 3.71 0.87
63 NNET_REC_NNET_SPEC9 Test 2.84 1.71 1.62 1.74 3.92 0.89
66 NNET_REC_NNET_SPEC12 Test 2.92 1.77 1.66 1.74 4.49 0.87
New York
1 BASE_REC_ARIMA_DEFAULT Test 3.09 1.16 1.30 1.16 4.41 0.94
3 BASE_REC_ARIMA_SPEC2 Test 3.09 1.16 1.30 1.16 4.41 0.94
30 BASE_REC_ETS_SPEC14 Test 3.18 1.19 1.34 1.17 5.06 0.95
San Diego
51 BASE_REC_STLM_SPEC3 Test 23.42 6.49 3.10 6.34 28.83 0.61
12 DEMOG_REC_ARIMA_SPEC1 Test 35.62 9.29 4.85 9.84 39.31 0.71
14 DEMOG_REC_ARIMA_SPEC3 Test 36.77 9.58 5.01 10.16 40.32 0.71

There’s a pretty good mix of models across the two tables including ARIMA, ETS (lots of this one), STLM, and neural-net. Among the ARIMA models there were some with the basic recipe and some with the recipe that included both economic and demographic variables.

Below are plots of forecasts of the test data period for each city using the best 3 global models.

Code 
top_3_global <- best_global_table |> slice_min(smape, n = 3) |> pull(.model_id)

hpi_mod_calib |>
  filter(.model_id %in% top_3_global) |>                            
  modeltime_forecast(                            
    new_data = testing(econ_splits),      
    actual_data = econ_data,                     
    conf_by_id = TRUE,                           
    keep_data = TRUE                             
  ) |>
  group_by(city) |>                             
  plot_modeltime_forecast(                      
    .interactive = FALSE,
    .title = "Forecast of Test Data",
    .facet_ncol = 1
  ) +
  theme(plot.title = element_text(hjust = 0.5))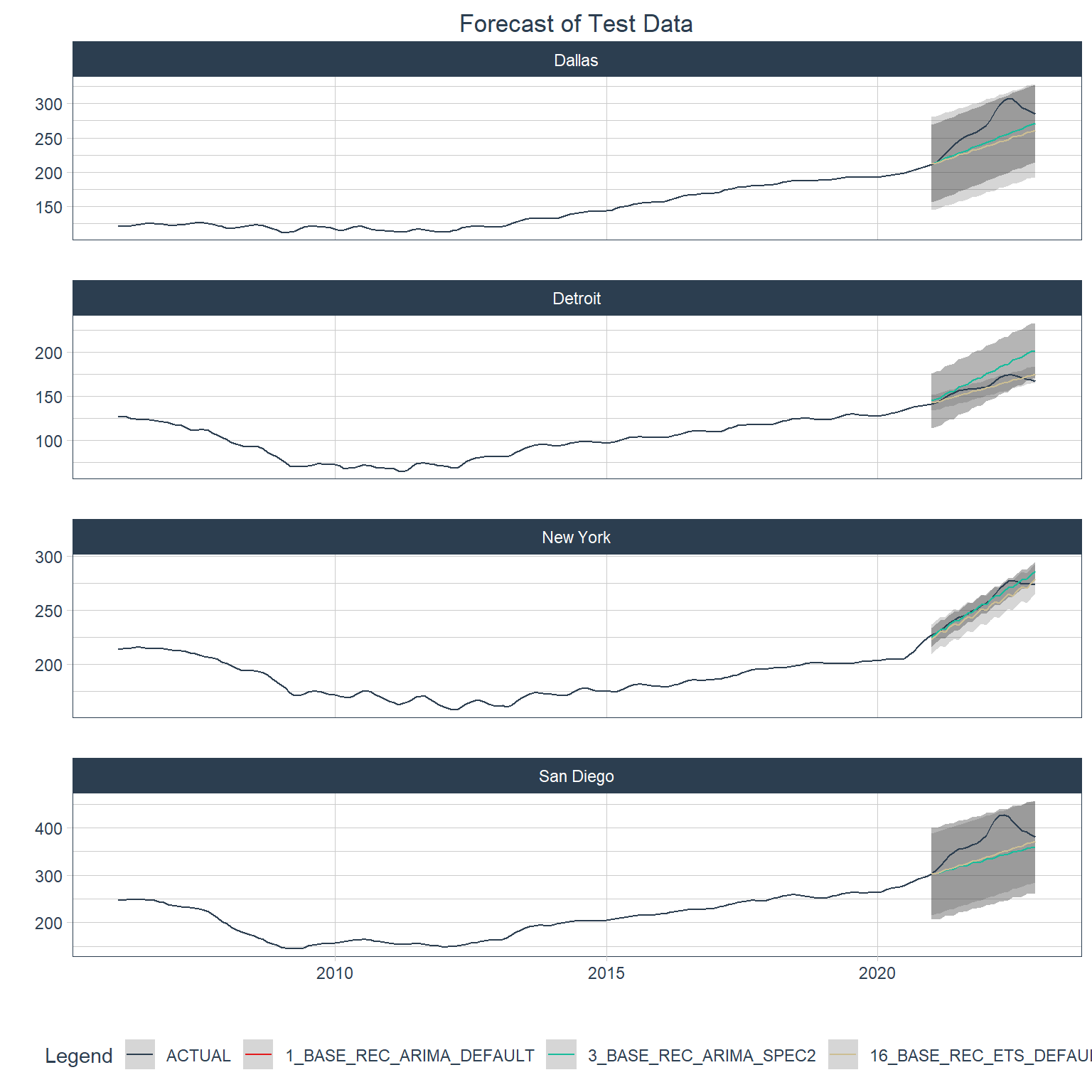
Figure 1

Just for fun, here are the 5 worst-performing models (global).

Code 
hpi_mod_accuracy |>
  slice_max(smape, n = 5, with_ties = FALSE) |>
  gt() |>
  gt_bold_head()
.model_id .model_desc .type mae mape mase smape rmse rsq
2 BASE_REC_ARIMA_SPEC1 Test 82.07379 28.40303 0.7639937 32.64595 100.22516 0.0237270639
4 BASE_REC_ARIMA_SPEC3 Test 81.85927 28.93424 0.7619969 32.63484 99.20593 0.0005985376
17 BASE_REC_ETS_SPEC1 Test 81.34845 28.53501 0.7572419 32.31949 99.36593 NA
19 BASE_REC_ETS_SPEC3 Test 81.34845 28.53501 0.7572419 32.31949 99.36593 NA
20 BASE_REC_ETS_SPEC4 Test 81.34845 28.53501 0.7572419 32.31949 99.36593 NA

Forecasting with global models

Below are forecasts for each city using the top 3 global models.

Code 
hpi_refit <- hpi_mod_calib |>
  filter(.model_id %in% top_3_global) |>
  modeltime_refit(data = econ_data) 

hpi_future <- econ_data |>
  group_by(city) |>
  future_frame(.length_out = 12, .bind_data = FALSE, .date_var = date)

hpi_future_forecast <- hpi_refit |>
  modeltime_forecast(
    new_data = hpi_future,
    actual_data = econ_data,
    conf_by_id = TRUE
  )

hpi_future_forecast |>
  group_by(city) |>
  plot_modeltime_forecast(
    .interactive = FALSE,
    .title = "1 Year Forecast into the Future - Global",
    .facet_ncol = 1
  ) +
  theme(plot.title = element_text(hjust = 0.5))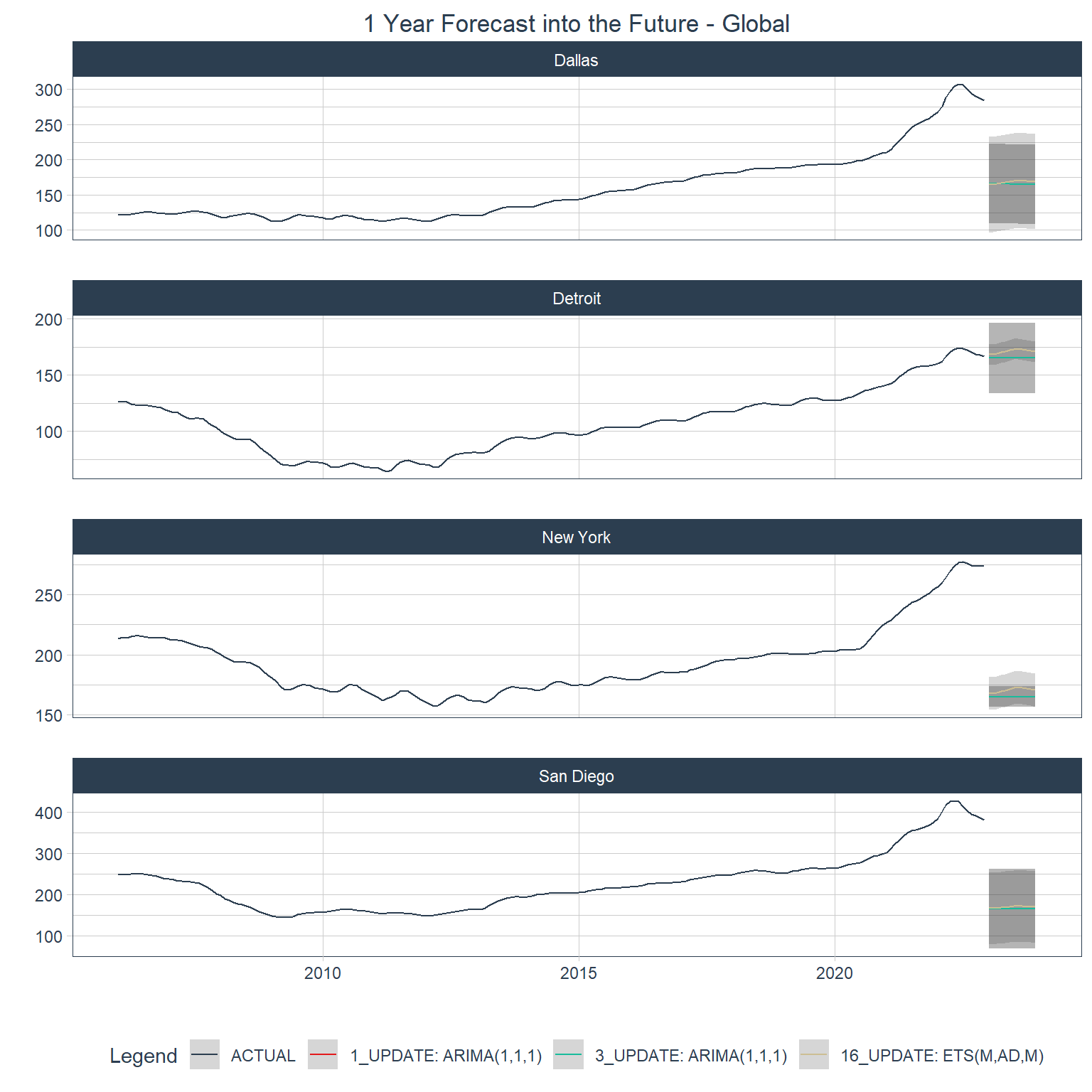

Choosing models for iterative process

For iterative modeling I’m going to use the 10 best global models and the 3 best local models for each city (there’s some overlap in these lists). The specifications that I’m going to use for iterative modeling in the next post are:

Code 
best_global_table |>
  slice_min(smape, n = 5) |>
  bind_rows(best_local_table) |>
  distinct(.model_desc) |>
  gt() |>
  gt_bold_head()
.model_desc
BASE_REC_ETS_DEFAULT
BASE_REC_ARIMA_DEFAULT
BASE_REC_ARIMA_SPEC2
BASE_REC_ETS_SPEC14
BASE_REC_ETS_SPEC6
DEMOG_REC_ARIMA_SPEC1
DEMOG_REC_ARIMA_SPEC3
NNET_REC_NNET_SPEC22
NNET_REC_NNET_SPEC9
NNET_REC_NNET_SPEC12
BASE_REC_STLM_SPEC3

References

Dancho, Matt. 2023. “Modeltime: The Tidymodels Extension for Time Series Modeling.” https://CRAN.R-project.org/package=modeltime.
Dancho, Matt, and Davis Vaughan. 2023. “Timetk: A Tool Kit for Working with Time Series.” https://CRAN.R-project.org/package=timetk.
Iannone, Richard, Joe Cheng, Barret Schloerke, Ellis Hughes, Alexandra Lauer, and JooYoung Seo. 2024. “Gt: Easily Create Presentation-Ready Display Tables.” https://CRAN.R-project.org/package=gt.
Kuhn, Max, and Simon Couch. 2023. “Workflowsets: Create a Collection of ’Tidymodels’ Workflows.” https://CRAN.R-project.org/package=workflowsets.
Kuhn, Max, and Hadley Wickham. 2020. “Tidymodels: A Collection of Packages for Modeling and Machine Learning Using Tidyverse Principles.” https://www.tidymodels.org.
Wickham, Hadley, Mara Averick, Jennifer Bryan, Winston Chang, Lucy D’Agostino McGowan, Romain François, Garrett Grolemund, et al. 2019. “Welcome to the Tidyverse” 4: 1686. https://doi.org/10.21105/joss.01686.